Funciones sobreyectivas

Una función es sobreyectiva, también llamada suprayectiva o exhaustiva, cuando el codominio y el recorrido coinciden. Formalmente:
∀y∈Codf ∃x∈Domf / fx=y
Es decir, para cualquier elemento y del codominio existe otro elemento x del dominio tal que y es la imagen de x por f.
Las funciones reales son sobreyectivas cuando Recf=ℝ, ya que, por definición, en ellas Codf=ℝ.
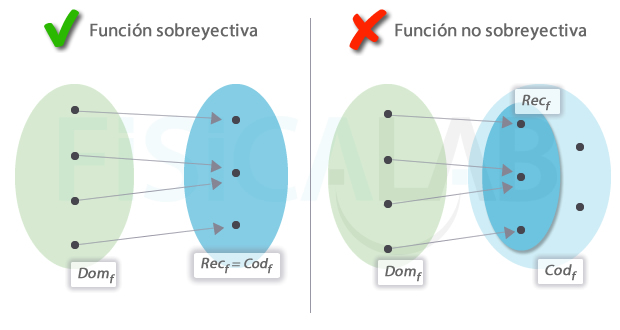
Función sobreyectiva y no sobreyectiva


Sobreyectiva vs no sobreyectiva

A la izquierda, una función sobreyectiva. Como tal, el codominio y el recorrido coinciden. O, dicho de manera más gráfica, todos los elementos del codominio reciben flechas. A la derecha, una función no sobreyectiva. En este caso hay elementos del codominio que no están incluidos en el recorrido. Observa, además, que ambas funciones son no inyectivas, pues ambas cuentan con elementos en el recorrido que reciben más de una flecha.
Resultado de imagen para graficas de sobreyectiva y no sobreyectiva


Resultado de imagen para graficas de sobreyectiva y no sobreyectiva

Comentarios

Publicar un comentario

Entradas populares de este blog

Imagen
Funciones biyectivas Una función es  biyectiva , cuando es inyectiva y sobreyectiva al mismo tiempo. Formalmente: ∀ y ∈ C o d f   ∃ ! x ∈ D o m f   /   f x = y Es decir, para cualquier elemento  y  del codominio existe un único elemento  x  del dominio tal que  y  es la imagen de  x  por  f . Biyectiva vs no biyectiva A la izquierda, una función biyectiva. Observa que cada elemento del recorrido recibe una (y solo una) flecha, con lo que  el número de elementos del dominio debe coincidir con el número de elementos del recorrido . En la ilustración superior derecha, una función que no es inyectiva, y por tanto tampoco biyectiva. En la ilustración inferior derecha, una función que no es sobreyectiva, y por tanto tampoco biyectiva.
Leer más
Imagen
Funciones inyectivas Una función es  inyectiva  cuando no hay dos elementos del dominio que tengan la misma imagen. Formalmente: ∀ a,b ∈ Domf , si fa= fb ⇒ a=b Es decir, para cualesquiera dos elementos  a  y  b , pertenecientes al dominio de la función  Dom f , si sus imágenes  f(a)  y  f(b)  son iguales, los elementos son necesariamente iguales. Inyectiva vs no inyectiva A la izquierda, una función que asocia a cada persona su altura. A cada elemento del recorrido llega una sola flecha, por lo que la función es inyectiva. A la derecha, la función también asocia a cada persona su altura. En este caso el dominio es ligeramente distinto, y cuenta con una persona más que, curiosamente, tiene la misma altura que el oficinista despreocupado de su peso (1.80m). Como a ese elemento del recorrido llegan dos flechas, la función ya no es inyectiva. Por tanto, si te piden una  demostración  de que...
Leer más