Funciones inyectivas

Una función es inyectiva cuando no hay dos elementos del dominio que tengan la misma imagen. Formalmente:

∀a,b∈Domf , si fa= fb⇒a=b

Es decir, para cualesquiera dos elementos a y b, pertenecientes al dominio de la función Dom_f, si sus imágenes f(a) y f(b) son iguales, los elementos son necesariamente iguales.

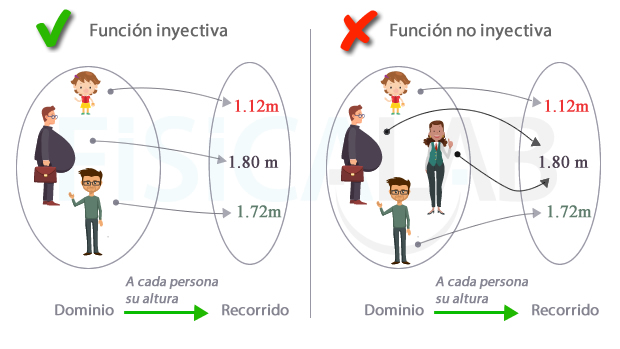
Inyectiva vs no inyectiva

A la izquierda, una función que asocia a cada persona su altura. A cada elemento del recorrido llega una sola flecha, por lo que la función es inyectiva. A la derecha, la función también asocia a cada persona su altura. En este caso el dominio es ligeramente distinto, y cuenta con una persona más que, curiosamente, tiene la misma altura que el oficinista despreocupado de su peso (1.80m). Como a ese elemento del recorrido llegan dos flechas, la función ya no es inyectiva.

Por tanto, si te piden una demostración de que una función no es inyectiva, puedes hallar dos valores distintos del dominio cuyas imágenes sean iguales. Si las encuentras, la función no es inyectiva.

En el caso de funciones reales, para saber si son inyectivas:

• Cuando están dadas mediante una ecuación, podemos utilizar la propia definición. Así, la función f(x)=2·x+1 es inyectiva, pues:
  $$\left.\begin{array}{r}f\left(a\right)=2a+1\\ f\left(b\right)=2b+1\end{array}\right\}\text{Si} f\left(\right)=f\left(\right)\Rightarrow 2a+1=2b+1\Rightarrow a=b$$
  Por otro lado, la función f(x)=x2 no es inyectiva pues:
  $$\left.\begin{array}{r}f\left(a\right)=a^2\\ f\left(b\right)=b^2\end{array}\right\}\text{Si} f\left(\right)=f\left(\right)\Rightarrow a^2=b^2\Rightarrow a=\pm b$$
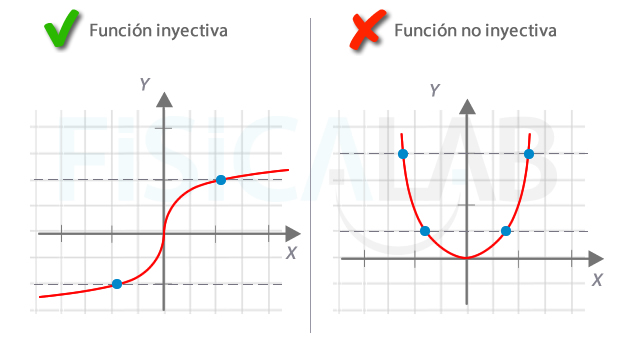
• Cuando están dadas gráficamente se trata de buscar dos imágenes iguales en la misma. Observa la siguiente ilustración y lo entenderás más claramente: